For a recent project, I needed the ability to estimate the distance to a detected object from a photograph. After some research, I stumbled upon the pinhole camera model, and implmented a Python library for performing the calculations to determine object distance based on that.
The model can be used to relate four variables to each other:
- “Real” object dimension
- Distance to object
- “Observed” object dimension
- Distance between aperature and sensor plane (Focal length).
pinhole-distance includes predefined “Packages” for three cameras I had on-hand. Using an object recognition model with the ability to output bounding boxes like YOLO, you can provide the observed width or height of an object, an estimate of what you believe the real width or height to be, and get an estimate
of how far away the object is.
How It Works
The pinhole camera model states that the ratio of the object dimension over the object distance is equal to the ratio of the observed dimension over the focal length. Expressed as an equation:
\[\text{let h = observed dim, d = focal length}\\\quad \text{H = object height, D = distance to object}\] \[\frac{\text{h}}{\text{d}}=\frac{\text{H}}{\text{D}}\]And, expressed as a drawing of dubious quality:
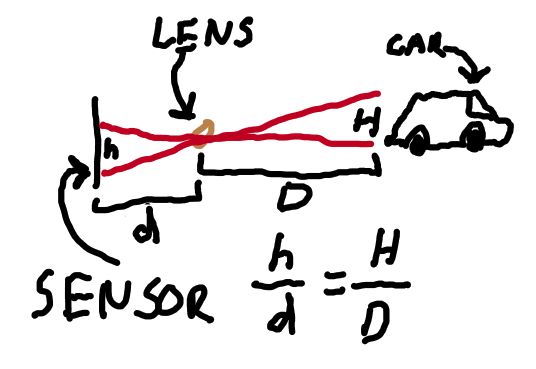
From this equation, we can:
\[\text{Solve for real distance, given H, h, d}\\\text{D}=\frac{\text{Hd}}{\text{h}}\] \[\text{Solve for object height, given D, d, h}\\\text{H}=\frac{\text{Dh}}{\text{d}}\]Manual Example
Let’s run through the math for the Raspberry Pi Camera 2. For the lens:
- No distortion (more on that later)
- 3.04mm focal length
The sensor:
- 1.12\(\mu\text{m}\) x 1.12\(\mu\text{m}\)
- 3280 x 2464 resolution
Let’s say we observe an object where \(H=1m\), and our observed measurement is 1000 pixels. First, we need to find \(h\), in meters:
\[\begin{eqnarray} h &=& 1000 * 1.12\mu\text{m} \\ &=& 1120\mu\text{m} \\ &=& 0.00112\text{m} \end{eqnarray}\]Since \(d\) is known, we can solve for distance now:
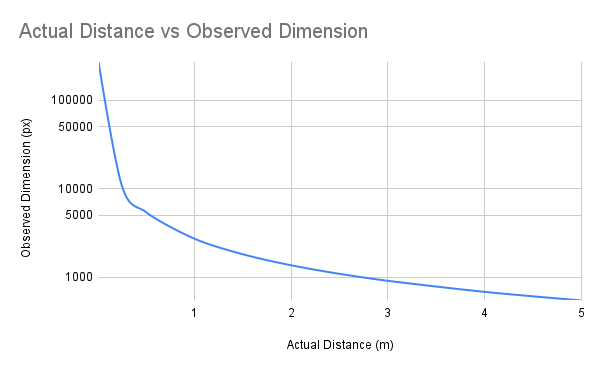
\[\begin{eqnarray} D &=& \frac{1\text{m} * 0.00304\text{m}}{0.00112\text{m}} \\ &=& \frac{0.00304\text{m}^2}{0.00112\text{m}} \\ &=& 2.714\text{m} \end{eqnarray}\]Working backwards, this makes sense. The sensor, at \(D=0\), would require \(1/0.00000112\) pixels, or roughly 900,000 pixels, to represent a one meter tall object. At \(D=1\), \(h=2714\text{px}\) and so on, following a curve as depicted below.
Distortion Compensation
One of the challenges with wide-angle lenses is image distortion (the “fish-eye” effect). Since surveillance cameras benefit from larger fields of view, this is a problem. The distortion causes objects near the edges of the frame to appear smaller than they actually are, resulting in inaccurate distance calculations. To compensate for this effect, I implemented a distortion correction system using a DistortionTable class that maps the relative position of an object from the center of the image to a correction factor. The correction factor is applied by determining what percentage of the maximum possible distance from the center the object is located (0.0 being at center, 1.0 being at the edge), looking up the corresponding correction factor, and then multiplying the calculated distance by (1 + distortion_factor). It supports rounding to arbitrary precision (e.g. round to the nearest 0.05 for the OV5647).
I’m not really sure how you’d figure out the distortion table on your own. The SparkFun data sheet for the OV5647-based camera package I used included one, so I didn’t have to worry about it all that much.
Supported Cameras
The library includes pre-defined configurations for three cameras:
- OV5647 - Arducam 5MP 120° wide-angle camera
- Includes distortion correction for the “fish-eye” effect common in wide-angle lenses
- RPI Camera Module 2 - The Raspberry Pi Camera Module v2
- USB Pinhole Camera - SVPRO 3.7mm Pinhole Lens USB Camera
You can also define your own camera packages using the library’s Sensor, Lens, and Package classes.
Code Example
First, install the package:
pip install pinhole-distance
Let’s say you’ve detected an object you know is 21 inches (0.5334 meters) wide, and it appears 70 pixels wide in an image from the USB pinhole camera:
# Calculate the distance to an object known to be 21" wide that is 70px wide in the image
from pinhole_distance import usb_pinhole
distance = usb_pinhole.distance_to_object(
dimension='x',
actual_dimension=0.5334, # Width in meters
observed_dimension_px=70 # Width in pixels
)
print(f"Distance to object: {distance:.4f} meters")
The output would be approximately 4.8986 meters, which is within 2% of the actual distance - and well within error bands for both measuring my own shoulder width and image recognition bounding box precision.
Conclusion
The pinhole camera model provides a straightforward way to estimate distances using only a camera, an object recogition model, and estimates on a detected object’s size. While it’s not as precise as specialized hardware like LIDAR or stereoscopic cameras, it’s fairly effective for a wide range of applications using standard camera hardware, with the added bonus of being completely passive.
The library is available on GitHub and PyPI, and I welcome contributions - particularly if you’ve calibrated distortion tables for other camera modules. For real-world applications, I’d recommend taking multiple measurements with known objects at known distances to establish your own error margins, as they can vary depending on the quality of your object detection model and the precision of your camera specifications.